Modelling the Mysteries of Magma Transport 

Tim Davis – University of Oxford, UK

---

Dyke and sill intrusions feed many volcanic eruptions, transporting magma from depth to the surface. These are magma-filled quasi-planar fractures that cut through rock masses, and their complex physical behaviour makes them very challenging to model. Over the last 100 years, our understanding of intrusion processes has come a long way. There have been major developments in analytical and numerical intrusion models, each shedding more light on the mysteries of magma transport. In particular, model development has, and continues, to be motivated by the following key open questions:

1. What path will magma take through the crust?
2. What causes magma to ascend and erupt?
3. What are the similarities between magma ascent and other associated processes, e.g. hydro-fracturing (fracking)?

My aim in this blog post is to take the reader on a timeline of intrusion model development, evolving from the simple analytical dyke models of the 20th century, to the three-dimensional numerical models of magma propagation which form the focus of my research today.

---

Pioneering origins

A series of key theoretical developments since the early part of the 20th century have quantified a theory for how dykes move and orientate themselves. Early models of intrusion orientations, developed in the late 1930s by EM Anderson [1], focused on the stresses around ellipsoidal cavities. These models showed that uniformly pressurised dykes align themselves in the direction of the most compressive stress. Following this pioneering result, fracture mechanics underwent a series of famous developments in the 1950s [2], based on some mathematical tricks used to relate strain energy to stresses. These developments provided key insights into when a material will break, and why materials are inherently weaker when they contain a fracture. Here is a short video I made of the mathematical tricks used to develop fracture mechanics theory in the 50s:

Buoyancy is key

More sophisticated models appeared in the 1970s [3], which included advances regarding fracture growth and density differences between the magma and the host rock, resulting in a buoyancy force. The theory states that if the dyke is over a certain height, it will rise through the crust by propagating through this. Analogue models of air injected into gelatine were undertaken in the late 80s, providing much-needed validation for the theoretical models. The experiments showed that fluid-filled cracks rise towards to the ground surface; provided there is a density difference between the fluid and host material. This process is akin to a helium balloon rising upwards due to buoyancy forces. One example of these experiments is shown here:

These models predict how long it takes a typical dyke to rise to the surface. One thing of note is that these models do differ from many gelatine experiments, as the models assume laminar flow inside the fracture. In many analogue gelatine experiments, this assumption is contradicted.

Unconventional dyke pathways

By the turn of the century, modellers had begun to focus on dyke pathways, exploring the routes intrusions take through the crust. Since the early works of EM Anderson, it was assumed that dykes always aligned themselves perpendicular to the least compressive stress direction, as this is the most efficient way to open the material surrounding a fracture. Numerical models in the early 2000s showed that the volume of fluid inside the dyke and its initial orientation define how long it takes for such fractures to re-orientate themselves to align with this stress [7,8]. Models that assume these fractures align along the most compressive direction remain a good first order assumption, as these can broadly explain many observations. More sophisticated fracture propagation models supply insights into the more nuanced variations in dyke pathways. Such pathways are observed in the gelatine analogue models of Delphine Smittarello and Francesco Maccaferri [9], shown below. Here an ascending air-filled fracture deflects due to a load placed on top of the gelatine, where the fracture with a smaller fluid volume deflects more than the larger one.

Fracking: industrial analogue

In the late 1990s, there was an industrial revolution in the United States (US), when an independent oil producer in Texas invented modern day fracking. They found that if large volumes of water were pumped into porous shales at high rates, followed by sand injection to hold the fractures open, the process produced commercial amounts of natural gas. The US oil and gas industry had known about the existence of these shale gas deposits for decades, but had failed to commercially exploit them. They had even resorted to detonating nuclear bombs within shale sequences several times in the 50s and 60s to try and extract this gas! Now that techniques to extract the gas commercially were available, the 2000s saw a boom in fracked gas. Note, this gas is still being sold as a ‘bridge fuel’ for the green energy transition, despite numerous studies showing that its use is untenable if we want to keep below the internationally agreed 1.5°C warming target and avoid climate breakdown.

In the context of understanding the mechanics of fluid-filled fractures, this shale revolution produced an abundance of analytical and numerical methods to simulate fluid-driven fracture processes, which dominated the literature in the 2000s [10]. These studies provide some key insights into the competition between viscous flow and fracture growth, quantifying how these interact during dyke growth. To date, many of these models neglect the key force driving magma upwards towards the ground surface – buoyancy.

Bringing it together – new research

During my PhD at the University of Potsdam, I revisited the two-dimensional critical-length dyke models of the 70s. The theory of a critical fracture length, which once exceeded causes magma to ascend through the crust by fracturing the rock above, is well quantified in two-dimensions (2D). However, the theory remains poorly constrained in three-dimensions (3D). I adapted the critical-length dyke model from 2D to 3D, developing rigorous definitions of the volume of fluid required before a fracture begins to ascend.

These 3D models – published in Geophysical Research Letters – show that relatively minor volumes of injected fluid can ‘run-away’ and rise upwards towards the surface. It’s worth mentioning that three other research groups independently published comparable formulations at around the same time [11,12,13]. The diagram below describes this theory; on the left, a helium balloon with a pair of scissors above this is trapped by a piece of string. Once enough helium is inside the balloon, its buoyancy force is large enough to allow the scissors to cut the string. Once this volume of helium is exceeded, if the string was a sheet of cloth (right image), this would rise and continuously cut upwards through this sheet.

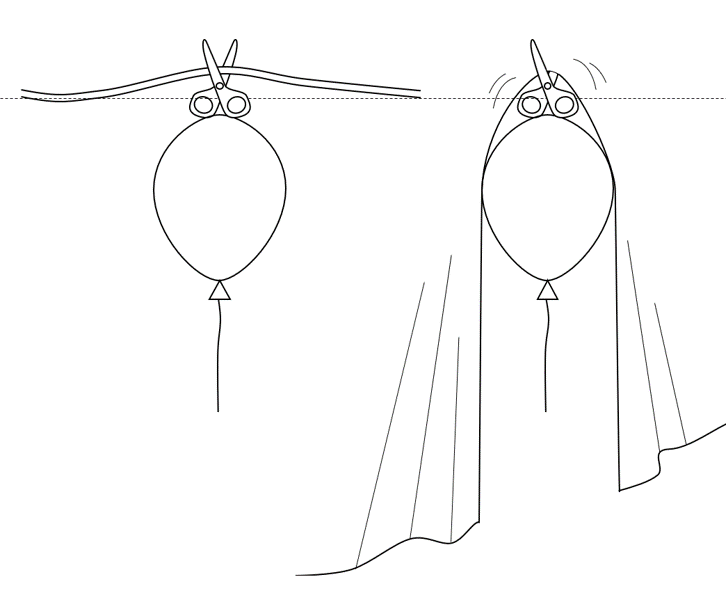
When applied to fluid storage in shale sequences, our results show that in some cases the amount of water required for fracture ascent is small, it would fit in a rubbish skip! For context, the UK government definition of hydraulic fracturing are operations where injection volumes are over 1000 cubic metres. This suggests that any water being pumped in to extract gas should begin to rise towards the surface. This has implications for the safety of industrial operations such as fracking or Carbon Capture Storage, which tend to assume that volumes of fluid stay put in the source rocks. There may be other processes acting to stop fluid ascent in shales, but there is currently no adequate quantitative description of these processes. I am currently working on quantifying the ability of different interfaces to trap ascending fractures, with the hope of understanding the conditions required to stop a fracture from reaching the Earth’s surface.

Until recently, simulations of magma pathways through the crust were all in 2D. In the latter stages of my PhD, I worked on numerical models of fractures reorienting themselves in stress gradients, and extended the 2D models to 3D using a boundary element code.

With colleagues at NASA, we applied this model to understand what processes led to a sill-fed eruption in the Galapagos islands, where the magma was observed to take an almost boomerang shaped path before erupting 10 km from the summit, out of the volcano’s flank. You can read about this work in our recent Geophysical Research Letters paper. Our model here assumed that there was a constant batch of fluid inside the sill. Our model was able to recreate the pathway of the intrusion prior to eruption, showing that such models are promising tools for understanding the journey of magma towards the surface.

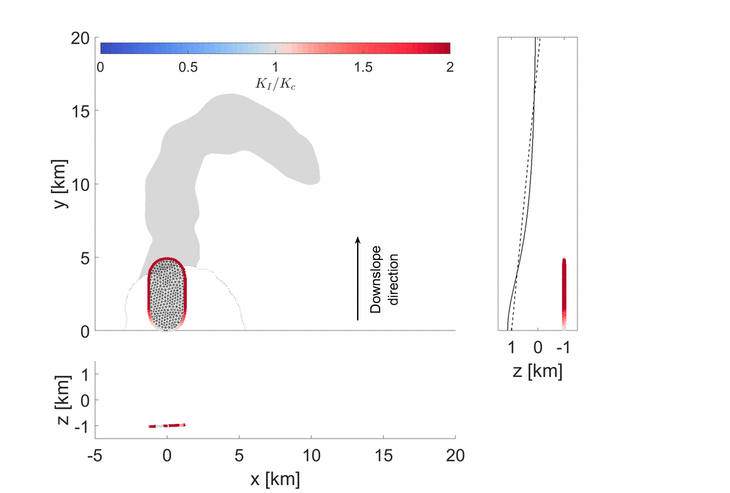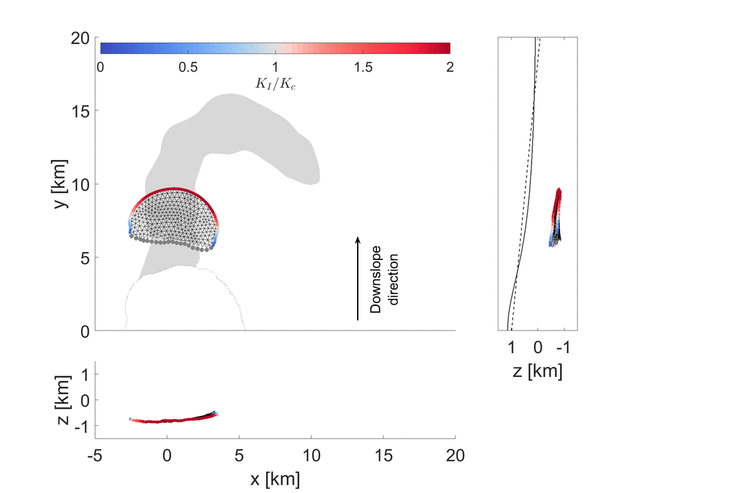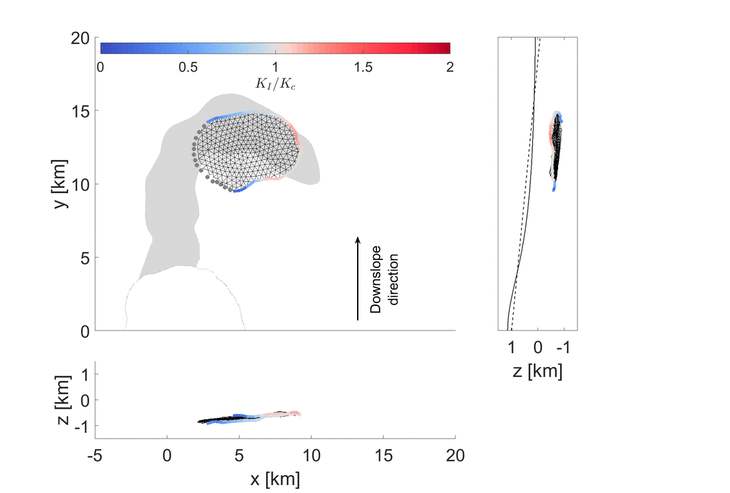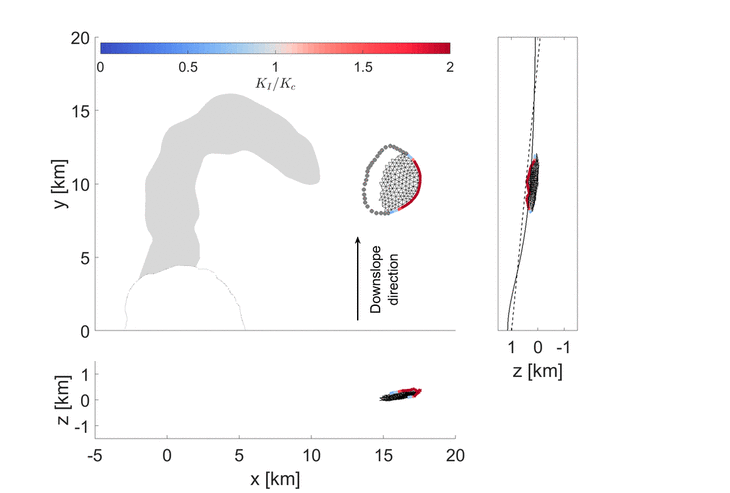
Many satellite observations show that the paths magma take before breaching the surface are tortuous. 3D models and simulations allow us to understand which parameters and associated forces define a given pathway, paving the way towards improved hazard assessment.

---

References

1. Anderson, E.M., 1939. XVII.—The Dynamics of Sheet Intrusion.
2. Irwin, G.R., 1957. Analysis of stresses and strains near the end of a crack traversing a plate.
3. Secor Jr, D.T. and Pollard, D.D., 1975. On the stability of open hydraulic fractures in the Earth’s crust.
4. Lister, J.R. and Kerr, R.C., 1991. Fluid‐mechanical models of crack propagation and their application to magma transport in dykes.
5. Rivalta, E., Böttinger, M. and Dahm, T., 2005. Buoyancy-driven fracture ascent: Experiments in layered gelatine
6. Spence, D.A. and Turcotte, D.L., 1990. Buoyancy‐driven magma fracture: A mechanism for ascent through the lithosphere and the emplacement of diamonds.
7. Dahm, T., 2000. Numerical simulations of the propagation path and the arrest of fluid-filled fractures in the Earth.
8. Muller, J.R., Ito, G. and Martel, S.J., 2001. Effects of volcano loading on dike propagation in an elastic half‐space.
9. Maccaferri, F., Smittarello, D., Pinel, V. and Cayol, V., 2019. On the propagation path of magma‐filled dikes and hydrofractures: The competition between external stress, internal pressure, and crack length.
10. Detournay, E., 2016. Mechanics of hydraulic fractures.
11. Salimzadeh, S., Zimmerman, R.W. and Khalili, N., 2020. Gravity hydraulic fracturing: A method to create self‐driven fractures.
12. Smittarello, D., Pinel, V., Maccaferri, F., Furst, S., Rivalta, E. and Cayol, V., 2021. Characterizing the physical properties of gelatin, a classic analog for the brittle elastic crust, insight from numerical modeling.
13. Möri, A. and Lecampion, B., 2021, October. Limiting Regimes of a Three-Dimensional Buoyant Hydraulic Fracture Emerging from a Point Source. (AGU Fall Meeting 2021).

---

---

---

Want to join us for our next ECR Coffee Time?

Did you know in January we launched a brand new monthly online ECR coffee time? This is a time for ECRs and students within the VIPS community to get to know each other chatting over a coffee (or other beverage) in the virtual world of Gather Town!

Our next coffee time will be on Thursday 3rd March at 3pm GMT (UK) / 4pm CET (Amsterdam) / 10am EST (New York). Join us here, and for more information click here.