3D Buoyancy-Driven Propagation of Hydraulic Fractures and their Applications to Magmatic Plumbing Systems

Andreas Möri and Brice Lecampion – EPFL Switzerland

Understanding how dykes behave as they propagate through the Earth’s crust has been a hot topic for VIPS researchers for many years – to see how magmatic intrusion models have evolved over the past century check out Tim Davis’ blog post! Through numerically modelling a planar three-dimensional (3D) fluid-filled fracture, mine and Lecampion’s research aims to provide insights into dyke emplacement mechanisms and the evolution of their shape.

Model Assumptions:
Our numerical model is based on the widely accepted assumptions of linear hydraulic fracture mechanics – the rock is assumed to be a linear elastic material with a constant fracture toughness, while the fluid flowing through the fracture is assumed Newtonian. The fracture toughness is a parameter that describes the resistance of solid material to fracture. We neglect any thermal processes and assume that the propagating magma does not leak into the surrounding rock formation. Additionally, we assume that the material properties are uniform and the gradient of confining stress is constant. The buoyancy force driving the fracture upward is equal to the difference between the gradient of confining stress and the fluid weight. We restrict the model to magma emplacement only, and we do not simulate magma cooling and solidification.

Two-dimensional (2D) models of buoyancy-driven hydraulic fractures are characterised by a head and tail structure that emerges as the fracture propagates. The head has a given constant shape, while the viscous flow within the elongating tail provides the dynamics of the dykes’ growth. Once the fracture has propagated for a long time, two-dimensional solutions predict either a viscosity- or a toughness-dominated regime for such a head and tail structure. In the viscous regime, most of the energy in the system is dissipated by the viscous pressure drop in the fluid, which occurs mainly in the tail. In the toughness regime, the dissipation of energy is primarily due to surface creation, which is controlled by the fracture toughness.

Interestingly, similar regimes are observed for 3D radial hydraulic fractures. Radial hydraulic fractures are viscosity-dominated at early times in their propagation, and transition towards toughness-dominated behaviour at later times (when the perimeter of the fracture and thus the expended fracture energy increases).

As part of our investigations, we utilise a scaling analysis to understand the interplay between the viscosity- and toughness-dominated limits when buoyancy forces are accounted for in radial fractures. Considering a magmatic point source injecting fluid into an impermeable rock at a constant rate, the propagation of 3D buoyant fractures from an initially radial shape is characterised by a dimensionless viscosity (denoted by ℳ_𝓀). This time-independent dimensionless viscosity parameter varies greatly for different fracture scenarios with different material properties and fluid injection rates (see Figure 1). Our research thus focuses on the delineation of intrusion characteristics as a function of this dimensionless coefficient, via simulations performed with the open-source 3D-planar hydraulic fracture solver PyFrac [1, 2].

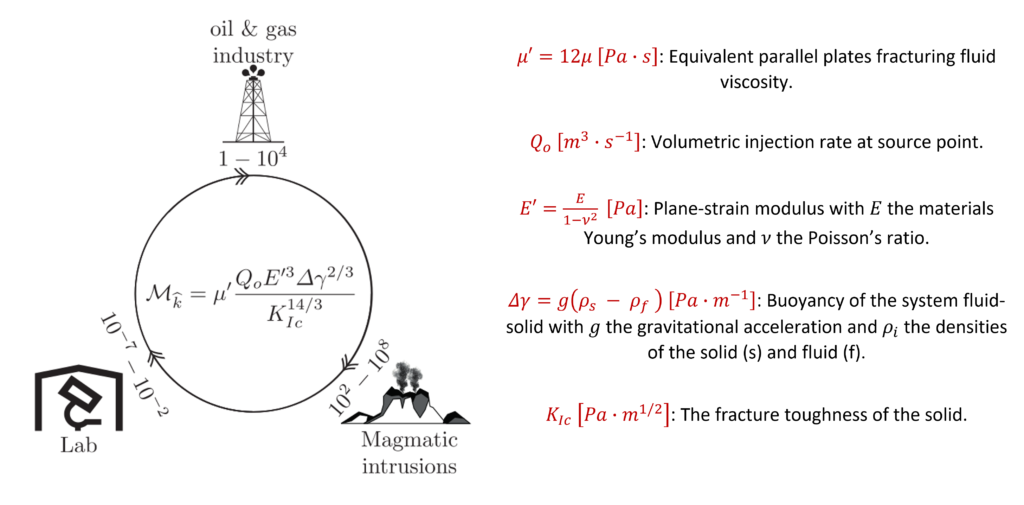
Figure 1: *Orders of magnitude of the governing dimensionless coefficient* ℳ_𝓀 *in the fields of application*.

Based on our 3D scaling analysis and numerical simulations, we identify the same limiting regimes as observed in two dimensions: a toughness dominated limit (when ℳ_𝓀 ≪ 1) and a viscosity dominated one (when ℳ_𝓀 ≫ 1). Model intrusions in the two regimes differ significantly in shape, ascent, and mass-flow rate. The difference in shape and ascent rate can be observed in Videos 1 and 2 below.

Toughness-Dominated Limit

Figure 2: Schematic representation of a buoyancy-driven hydraulic fracture with a large fracture toughness in its late state. The sketch is based on a late-time snapshot of the simulation presented in Video 1.

Video 1 corresponds to an intrusion with a large fracture toughness (ℳ_𝓀 ≪ 1): the resulting intrusion is finger-like with a constant breadth. From the dynamics of the video, we observe that the fracture shows a very strong acceleration phase when the buoyancy-driven propagation starts. This transient phase dominates the growth for a very long time and is likely to persist over the entire subsurface propagation. A direct consequence is that the ascent rate requires very long propagation times and distances to become constant. The late-time constant ascent rate predicted by theory might thus never actually be reached in laboratory experiments, nor in real magmatic intrusions. A very marked feature of the toughness-dominated fracture is its head – the red coloured section at the top of the propagating dyke in Figure 2 and Video 1. The volume of the head remains constant, whereas the rest of the fracture reduces to a thin conduit (the tail), connecting the injection point source to the head. These observations seem to coincide well with buoyancy-driven fractures in laboratory experiments [3, 4, 5].

Viscosity-Dominated Fracture

In volcanic plumbing systems, dykes are more likely to be in the viscosity-dominated regime (ℳ_𝓀 ≫ 1). The teardrop-shaped fracture of Video 2 is more like what we expect in volcanic plumbing systems. The simulation in the video demonstrates a clear decrease in ascent rate with time, as predicted by the theory. In this viscous limit, the lateral extent of the fracture increases with time, and is independent of the fracture toughness of the material. This is a striking difference compared to results from 2D models, which intrinsically cannot capture the dynamics of dyke growth in the third dimension.

Our numerical results indicate that the shape of the established dyke becomes self-similar at later times of propagation. The self-similar dyke structure includes a head with a stable shape but a shrinking volume (this shrinking is barely visible in Video 2). Contrary to the toughness-dominated case, the bulk of the fluid volume resides in the tail – not in the head. The self-similarity establishes only when the volume of the head becomes negligible compared to the one in the tail. Even for large (but finite) values of dimensionless viscosity (e.g. ℳ_𝓀 ∈ [10²−10³]), such a self-similarity is never reached, because a finite value of fracture toughness limits the lateral extension of the dyke.

An intrusion with a large fracture toughness (ℳ𝓀 ≪ 1), resulting in a finger-like intrusion with a constant breadth — Video 1: An intrusion with a large fracture toughness (ℳ_𝓀 ≪ 1), resulting in a finger-like intrusion with a constant breadth

Teardrop-shaped fracture, more similar to what we expect in volcanic plumbing systems (ℳ𝓀 ≫ 1) — Video 2: Teardrop-shaped fracture, more similar to what we expect in volcanic plumbing systems (ℳ_𝓀 ≫ 1)

Despite our model strongly simplifying the propagation of magmatic intrusions, some interesting insights still emerge. We can notably show that the shape, ascent style, and mass-flow rates of dykes strongly depend on the material properties and magma release rate. We can further show that the transition to buoyancy-driven propagation from a radial fracture is very important for buoyant fractures emerging from a point source. This transition is likely to govern laboratory experiments and magmatic intrusions over the entire duration of the fracture propagation. Furthermore, our model allows us to identify a self-similar behaviour in viscosity-dominated fractures at late times in propagation.

Defining this simple problem as precisely as possible was our starting point, before adding more complex physics to our model. Currently we’re considering the case of the release of a finite volume of fluid, and we are further characterising the late-time self-similar behaviour in viscosity-dominated dykes with a continuous injection rate. Additionally, we’re investigating the effects of having heterogeneities in fracture toughness, rock density, and confining stresses (see Video 3 where a jump in confining stress prevents the upward propagation of the fracture).

Video 3: A jump in confining stress prevents the upward propagation of the fracture

My future research goals are to include cooling, leaking of the fluid in the surrounding host rock, propagation arrest and subsequent closure, and eventually poroelastic effects. We hope that this complete picture of emplacement and cooling will ultimately lead to a general understanding of the three-dimensional emplacement of magmatic intrusions in nature. You can find more information on the topic in our AGU Fall Meeting 2021 poster. A manuscript on these findings is in preparation, follow us on our webpage or keep an eye out on our Twitter for the preprint!

References

Andreas Möri (andreas.mori@epfl.ch) is currently in the third year of his PhD at EPFL in Switzerland. Prior to his PhD, he studied an MSc in Civil Engineering with specialisations in Geotechnics and Structures.

Currently Andreas’ research focuses on the investigation of buoyant processes and poroelasticity in hydraulic fracture mechanics. He uses numerical models and analytical tools to gain insight into the fundamental processes of the growth of such fractures. The applications of his research varies from the stimulation of well production in geo-energy projects to the transport of magma in the crust!

If you’re interested Andreas’ research or just want to chat, you can get in contact with him via Twitter or by email.

Would you like to be featured on our blog?

We are on the hunt for fellow VIPS enthusiasts to share their stories, whether you’re a student, an early career researcher (ECR) or more experienced researcher – we want to hear from you!

Do you have a new paper to tell the world about? Or have you been involved in some exciting fieldwork recently? Get in touch at info@vipscommission.org to tell us what’s going on in your field of VIPS.

Share this post:

Twitter Facebook Pinterest LinkedIn E-mail